|
ЭКСПЕРИМЕНТ
11 Теорема Тевенина-Гельмгольца
Цели
После проведения данного
эксперимента Вы сможете продемонстрировать и проверить теорему Тевенина-Гельмгольца
и использовать ее для анализа схем.
Необходимые принадлежности
* Цифровой мультиметр
* Макетная панель
* Источник постоянного
напряжения
* Резисторы — 1/4 Вт, 5%:
один резистор 470 Ом, один
резистор 1 кОм, один резистор 2, 2 кОм, один резистор 3, 3 кОм.
ВВОДНАЯ ЧАСТЬ
Теорема Тевенина-Гельмгольца
в значительной степени облегчает анализ и разработку электронных схем. Эта теорема
позволяет Вам заменить сложную схему, включенную между источником питания и
нагрузкой, единственным последовательно включенным резистором. Для примера,
предположим, что Вы желаете проанализировать работу схемы, представленной на
рисунке 11-1.
Постановка задачи
Конкретно Вы желаете узнать
нагрузку или выходное напряжение для различных значений сопротивления нагрузки
RL. Всякий раз, когда Вы изменяете RL, Вам надо найти полное сопротивление и
общий ток, токи в ветвях и падения напряжения. Этот процесс несложен, но утомителен
и требует затрат времени.
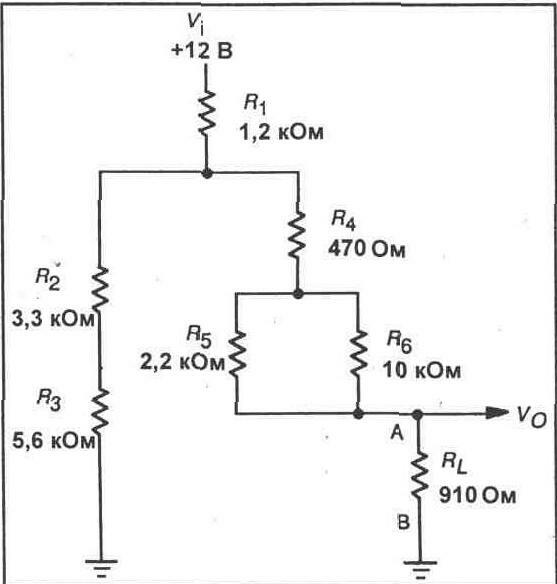
Рис. 11-1.
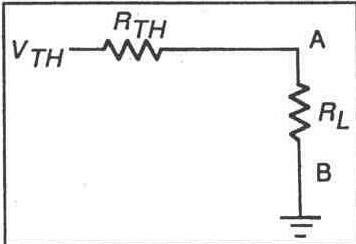
Рис.
11-2.
Решение
Используя теорему Тевенина-Гельмгольца,
можно заменить всю сложную схему, включенную между источником питания и нагрузкой,
единственным последовательно включенным резистором с сопротивлением, которое
называется эквивалентным сопротивлением Тевенина, R . Источник питания заменяется
источником питания с другим напряжением, величина которого называется эквивалентным
напряжением Тевенина, Vтн (см. рис. 11-2).
В своей совокупности эквивалентное
напряжение Тевенина и эквивалентное сопротивление Тевенина формируют напряжение
на любой нагрузке и ток в ней с теми же значениями, которые формируются и оригинальной
схемой. В результате схемный анализ становится значительно более простым, поскольку
весь расчет теперь сводится к расчету простой последовательной схемы.
Шаги
Самый легкий способ для
определения эквивалентов Тевенина — это их измерение в конкретной схеме. Чтобы
сделать это для рисунка ll-l, удалите нагрузку и, при наличии приложенного
напряжения источника питания,
измерьте напряжение между точками включения нагрузки А и В. В результате Вы
получаете эквивалентное напряжение Тевенина Vтн.
Далее, при все еще удаленной
нагрузке, отсоедините напряжение источника питания и замените его короткозамыкателем
(перемычкой). Затем измерьте сопротивление между точками включения нагрузки
А и В. В результате Вы получаете эквивалентное сопротивление Тевенина R
После этого Вы можете фактически
собрать эквивалентную схему Тевенина с варьируемым источником питания, настроенным
на величину напряжения Vтн, и выбрать стандартный резистор с сопротивлением
ближайшим к Rтн. Теперь Вы можете подключать различные нагрузки и смотреть,
как они работают.
Схемные значения
Другим методом является
нахождение величин Vтн и Rтн. Ha основании схемных значений. Сначала удалите
резистор нагрузки RL и рассчитайте, напряжение, которое появляется на контактах
А и В. Для схемы, представленной на рисунке ll-l, при удалении RL, резисторы
R4, R5 и R6 остаются открытыми. Как результат, приложенное к резисторам R2,
и R3 напряжение появляется между контактами А и В.
Vтн = Vав
= 12 (R2 + R3)/(R1 + R2 + R3) Vтн=Vав = 12 (8,9/10,1) = 12(0,881) = 10,6 В
Далее рассчитывается
Rтн. При удаленном R источник питания 12 В заменяется короткозамыкателем. Вычисляется
сопротивление между точками А и В.
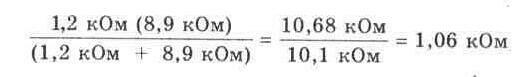
R4 последовательно
с соединенными параллельно резисторами R5 и R6
1,8 кОм +
0,47 кОм = 2,27 кОм
Эквивалентное сопротивление
между точками А и В:
Rтн =
2,27 кОм + 1,06 кОм = 3,33 кОм
Эквивалентом Тевенина является
источник постоянного напряжения 10,6 В, соединенный последовательно с сопротивлением
3,33 кОм.
Теперь при подключении
к этой цепи резистора R, получается полное сопротивление:
910 + 3330
= 4240 Ом
Полный ток, протекающий
через схему, имеет величину:
10,6 / 4240 = 0,0025 А
= 2,5 мА
А падение напряжения на
RL равно:
10,6[910/(910 + 3330)]
= 10,6(910/4240) = 2,28 В
Краткое содержание
В данном эксперименте Вы
будете использовать процедуру, приведенную ниже.
ПРОЦЕДУРА
1. Обратитесь к схеме,
представленной на рисунке 11-3. Используя показанные значения, выполните
расчет эквивалентного напряжения и эквивалентного сопротивления Тевенина в точках
А и В. Вычислите выходное напряжение для сопротивления нагрузки 3,3 кОм.
Vтн = ____ В
Rтн = ______ Ом
VL=____В
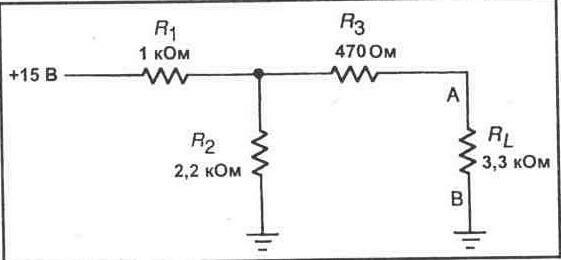
Рис. 11-3.
2. Соберите схему, показанную
на рисунке ll-З. Включите питание и измерьте эквивалентное выходное напряжение
Тевенина на контактах А и В без нагрузки.
Vтн (измеренное) = ______
В
3. Включите нагрузку 3,3
кОм между точками А и В. Измерьте теперь выходное напряжение. Как оно сравнивается
с Вашим расчетным значением?
VL (измеренное)
= ____ В
4. Выключите питание. Отсоедините
источник питания. На его место включите проволочный короткозамыкатель. Отсоедините
также нагрузку от контактов А и В. Затем мультиметром
измерьте эквивалентное
сопротивление Тевенина на контактах А и В.
Rтн (измеренное) =
____ Ом
5. Нарисуйте эквивалентную
схему Тевенина и укажите на ней значения. После этого соберите эту схему, используя
источник питания и 'резистор. Используйте такой стандартный резистор, сопротивление
которого ближе всего к эквивалентному.
6. Включите питание и измерьте
выходное напряжение Тевенина. Отрегулируйте напряжение источника питания, чтобы
получить значение, которое Вы рассчитали в шаге 1.
7. Подключите нагрузку
3,3 кОм к эквивалентной схеме и измерьте выходное напряжение. Оно такое же,
как и то, которое Вы получили в шаге 3? Объясните.
ОБЗОРНЫЕ
ВОПРОСЫ
1. Почему на рисунке 11-1
при удаленном резисторе RL, комбинация резисторов R4-R5-R6 не влияет на выходное
напряжение?
а) фактически она влияет
на выходное напряжение,
б) в них не протекает ток
или на них нет падения напряжения,
в) сопротивление этой комбинации
намного меньше, чем сопротивление RL, поэтому нет влияния на выход.
2. Какое значение сопротивления
нагрузки создаст максимальную мощность в нагрузке?
а) 910 Ом,
б) 1,06 кОм,
в) 3,33 кОм,
г) 10,6 кОм.
3. Для вычисления Vтн,
резистор RL:
а) удаляется или его контакт
размыкается,
б) закорачивается.
4. Для вычисления Rтн,источник
питания:
а) отключается одним выводом,
б) закорачивается.
5. Теорема Тевенина используется
как для схем переменного тока, так и для схем постоянного тока:
а) высказывание истинно,
б) высказывание ложно.
|